閾値とは、刺激を与えるときに、感覚の内容が変化する境目での刺激の物理量のことである。たとえば、音の大きさをだんだん小さくしていって、音が聞こえなくなったとすると、その時の音の大きさの物理量が、音を検知する際の閾値(検知閾)である。
弁別とは、2つの刺激の間の差異の序列を聞き分けたり見分けたりする働きである。弁別限(弁別閾ともよぶ)とは、2つの物理量の異なる刺激を与えるときに、刺激に対する感覚の違いがわからなくなる境目での刺激の物理量の違いのことである。たとえば、周波数の異なる2つの音を呈示するときに、どちらの音の高さが高いか、わからなくなる境目での周波数差が、音の高さの弁別限である。
一般的に、閾値や弁別限付近での感覚は連続的に変化しており、その値を境に、スッパリ感覚の内容が変わったり、変化がわからなくなったりは、しない。このため一般的には、全く変化がわからないときの刺激の物理量と、明らかに変化が分かるときの刺激の物理量との中間に、閾値や弁別限が存在すると考えられている。
ある感覚についての特定の条件においての弁別限を知ることは、その条件下では、その感覚は物理量の変化にどれだけ敏感であるか、を知ることになる。つまり弁別限が小さいほど、敏感である、ということになる。また、なぜ敏感なのか、そうでないのか、の理由を考えることによって、感覚情報処理のしくみを間接的にではあるが、推測することも可能である。
刺激の物理量と、その刺激によってうける反応(通常は強制選択法での正答率)との関係をあらわす関数。精神測定関数や、刺激特性曲線などとも呼ぶ。
二肢強制選択法(2 Alternative Forced Choice Task : 2AFC法)によって実験を行うことを考える。たとえば、
のような課題が考えられる。
1つめの課題は、物理的に周波数が異なる2つの音に対して、音の高さの感覚はどこまで正確に判断されるか(周波数弁別能力)、を調べるものである。2つめの課題は、ある音によって目的音の聴取が妨害される(マスキングという)ときの、目的音がどこまで小さい音で聞こえるか(聴取閾値)を求める実験である。3つめは音色の弁別能力を調べる際などに行われる2AFC法のひとつである。
これらの課題においては、完全に正解が分かる時には正答率は100%に近くなる。一方、全く分からず適当に答えても、選択肢は2つであるから、半分は正答できる。このような、つまり正答率が100%に近い時の刺激の物理量と、50%に近いときの刺激の物理量との間に閾値や弁別限が存在する。通常は、75%の正答率となるときの刺激の物理量を、閾値や弁別限とすることが多い。
得られた正答率を縦軸に、横軸をその正答率を与える刺激の物理量として、グラフを描いてみる。このグラフが、心理測定関数に相当する。
閾値や弁別限を求める方法はいくつか存在する。ここでは、心理測定関数を直接測定する実験手法である恒常法を用いて閾値や弁別限を求める方法について説明する。
刺激の物理量をいくつか(通常3〜7レベル)選び、そのそれぞれの刺激レベルにおいて、2AFC法などを用いて刺激を多く(通常10回以上)呈示し、得られた回答の正答率を調べるような測定方法。刺激の呈示は順序効果を無くすために、ランダムな順序で行われる必要がある。
恒常法によって行われた実験の結果は、刺激の物理量とそのときの正答率とが組み合わされたデータであらわされる。このデータに適当な関数を当てはめ、正答率が75%となるときのその関数の値を計算して、その値を閾値や弁別限とする。ここでの適当な関数とは、通常は正規分布の累積関数などが考えられるが、最も簡単な関数は直線である。
次に、心理測定関数にロジスティック関数を用い、最尤推定法という算法を用いて、正答率の点にもっともフィットするような心理測定関数を算出して、閾値あるいは弁別限を計算するプログラムの使用方法を説明する。
まず、測定結果のデータファイルを作成する。この例でのデータファイル名は test.dat とする。
2 0 0.55 1 0.66 2 0.72 3 0.84 4 0.97
最初の行は選択肢の数を示し、2行目以降は、1行につき、
[刺激の物理量] [正答率]
のならびになっている。MS−DOS窓を起動して、データファイルのあるディレクトリに移動し、
mcsfit test.dat
のようにプログラムの引数にデータファイルを与えて実行すると、結果が表示される。
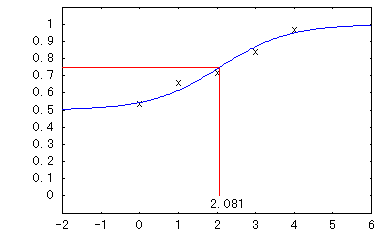
2 alternative forced choice task level score 0.000 0.540 1.000 0.660 2.000 0.720 3.000 0.840 4.000 0.970 Iteration 41 Slope 1.128 75.00% Threshold 2.0806 Max of function 2.513
75.00% Threshold
の右に表示される値が75%正答率を与える閾値あるいは弁別限となる刺激の物理量である。
mcsfit test.dat test.gp
のように2つめの引数となるファイル名を与えると、そのファイル名で gnuplot のプロットファイルができあがる。 gnuplot を起動して、
cd "データファイルのあるディレクトリ" load "test.gp"
のようにすれば、正答率、閾値、心理測定関数の形をグラフで見ることがで きる。

上記の例は、測定点間の刺激の物理量が等間隔 (1 2 3 4 5 のように)となる場合であるが、対数等間隔(たとえば、0.1 0.2 0.4 0.8 1.6 3.2 のように2倍づつ変化するような)の刺激を用いた場合は、とりあえず、(0 1 2 3 4 という)等間隔の値に刺激の物理量を変えて計算を行う。得られた閾値あるいは弁別限の値を x とし、初期値が y で a倍づつ変化する刺激の弁別限は、
y×(a の x乗)
を計算することによって求まる。
例えば、先ほどの test.dat の正答率のデータは刺激の物理量がそれぞれ、0.1 0.2 0.4 0.8 1.6 のときに得られたものだとすると、対数軸上での閾値あるいは弁別限の値は、
0.1 × (2 の 2.08乗) = 0.4228
となる。